Démonstration du théorème de Brouwer :

On prend \(f:B^\prime(0,1)\to B^\prime(0,1)\) continue, et on suppose par l'absurde quelle ne possède pas de point fixe.
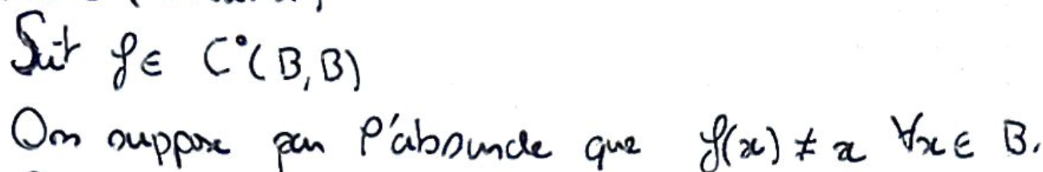
On définit l'ensemble des translations de \(x\) par \(\lambda(x-f(x))\), avec \(\lambda\geqslant0\), qu'on intersecte avec la frontière de la boule unité pour avoir \(\varphi(x)\).
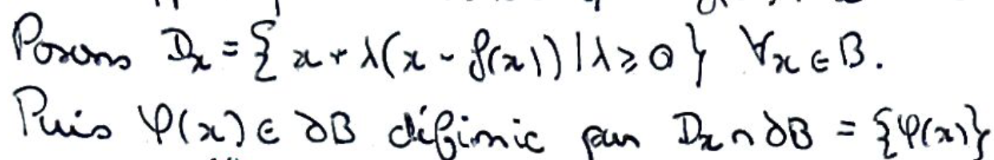
\(\varphi\) est continue en tant que racine positive d'un polynôme de degré \(2\).
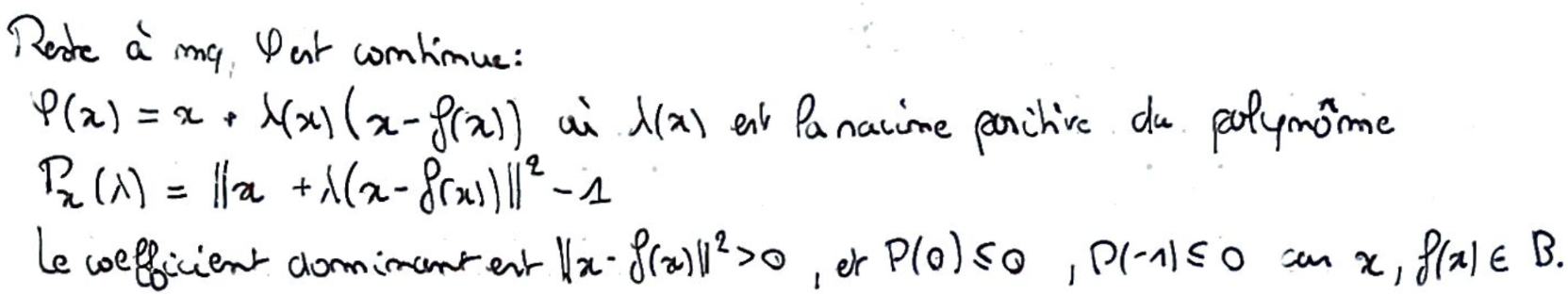
Alors \(\varphi\) n'a que des points fixes sur la frontière de la boule unité, ce qui contredit le Lemme de non-rétractation.
